声明
特别声明:本文章中所有内容仅供学习交流,不可用于任何商业用途和非法用途,否则后果自负,如有侵权,请联系作者立即删除!由于本人水平有限,如有理解或者描述不准确的地方,还望各位大佬指教!!
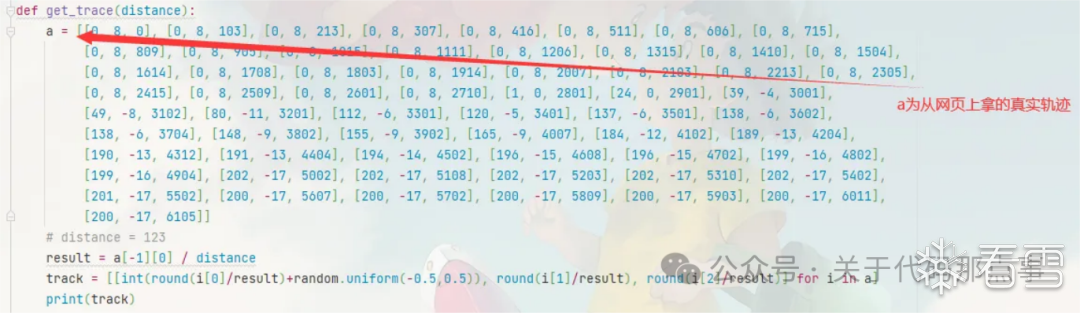
录制轨迹
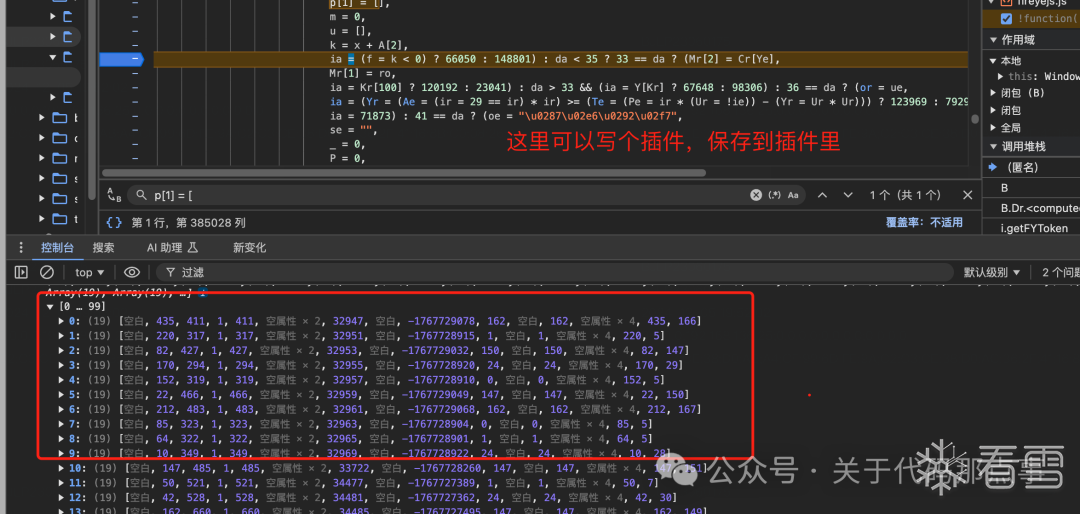
其实这是一个比较原始的方式,我在最早做某音滑块的时候因为不会写轨迹算法,就选择一条一条在网址滑动录制下来,依稀记得我滑了一晚上,成功率还感人,不到百分之二十......但是这个需要看用什么场景,例如一些滑动到底的滑块就很好应用,是的没错,就是我们的老朋友某里231与某团的,这里短暂看一下先看一下某里的(后面会单独出一个某团的滑块文章详解),我最早做140,223的时候就选择这个方法,巨好用,当时自己也差不多滑了一晚上,存了几万条随取随用,唯一不好的就是太笨重了,整个项目很臃肿。
缩放轨迹
其实简而言之,也类似录制轨迹,只不过唯一不同的这个相对于缺口滑块的成功率会更高,当初某盾与某数就是这么做的,网址多滑动几次轨迹,以此保存下来,按照识别滑块的距离使用不同比例的缩放,这里我简单示范一下1.从⽹站上拿⼀条真实轨迹,然后对该轨迹进⾏操作2.滑动滑块(尽量拉到底),先在js中跟栈,然后找出该次滑动对应的坐标以及轨迹3.进⾏缩放,⽐如拿到的轨迹对应的坐标是250,那么当坐标为150时,两个轨迹的倍数就是250/150,然后按照这个倍数对250的那条轨迹进⾏整体缩放
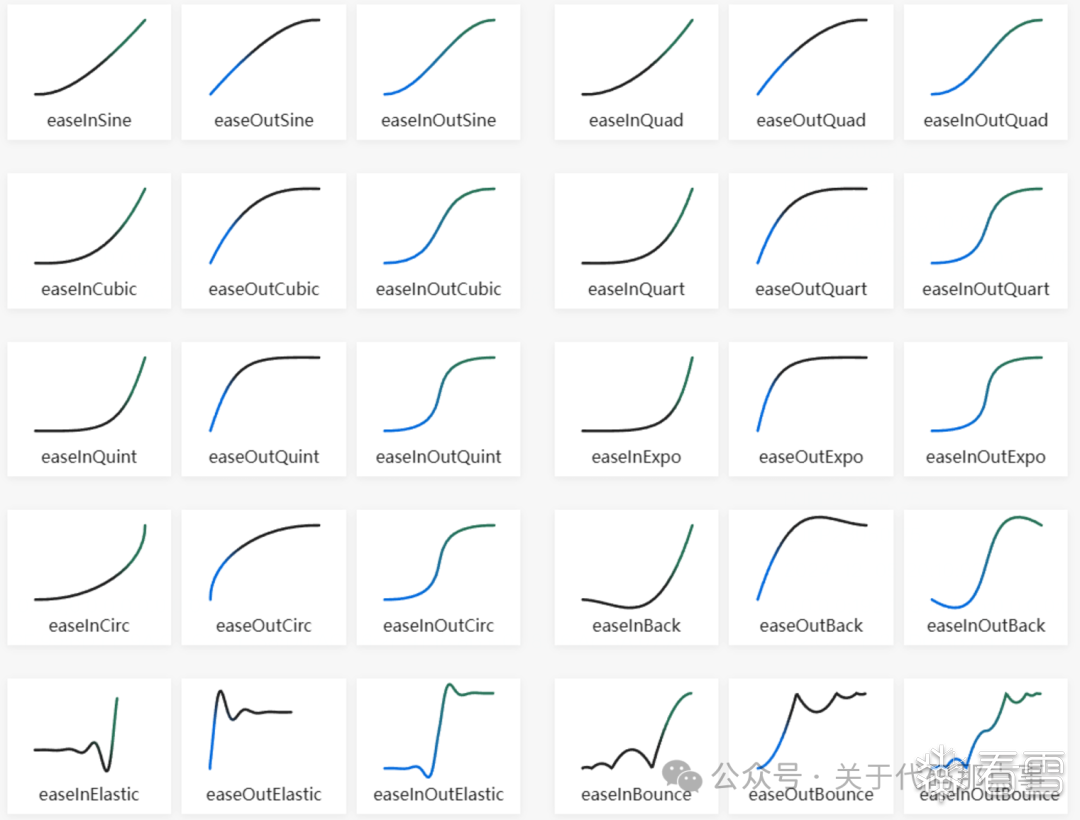
缓动函数
在简述了上面两种方式后,这里已经对轨迹有逐步的解了,但是以上两种只能针对一些风控较弱或者特定的一些场景,到了这里如果一些网址开始加强一些风控的时候,那么这两个方案就不在生效了,那么这个时候就开始需要一些拟人的特征,那么在初步的风控中也就可以应用到缓动函数了。这里先简单了解一下什么是缓动函数:BackEase:动画开始在指定路径上运动前稍微收缩动画的运行。BounceEase:创建弹跳效果。CircleEase:使用圆函数创建加速和/或减速的动画。CubicEase:使用公式 f(t) = t3 创建加速和/或减速的动画。ElasticEase:创建一个动画,模拟弹簧的来回振荡运动,直到它达到停止状态。ExponentialEase:使用指数公式创建加速和/或减速的动画。PowerEase:使用公式 f(t) = tp 创建加速和/或减速的动画,其中 p 等于 Power 属性。QuadraticEase:使用公式 f(t) = t2 创建加速和/或减速的动画。QuarticEase:使用公式 f(t) = t4 创建加速和/或减速的动画。QuinticEase:使用公式 f(t) = t5 创建加速和/或减速的动画。SineEase:使用正弦公式创建加速和/或减速的动画。缓动函数之前多数应用于动画场景,用于控制动画过渡过程中的速度变化,通过不同的函数曲线使得动画看起来更自然与流畅,但是其中有最为关键的一点:自动加减速,那么能做这一点就可以用到逆向领域了,我们可以在网址手动滑动一下,用python自带的画图库画出来,看一下轨迹的一个波动曲线,在针对下图进行代码轨迹特征进行适配,来找到一个最为相似的进行编写。这里我简单放几个缓动函数的算法,大家可以参考一下easeInSine
function easeInSine(x: number): number {
return 1 - cos((x * PI) / 2);
}
easeOutSine
function easeOutSine(x: number): number {
return sin((x * PI) / 2);
}
easeInQuad
function easeInOutSine(x: number): number {
return -(cos(PI * x) - 1) / 2;
}
在这里我就不多简述了,我在星球中会有更详细的解释
贝塞尔曲线
首先我们先来了解一下什么是贝塞尔曲线:贝塞尔曲线是一种用数学公式定义的参数化曲线,广泛应用于计算机图形学、动画、矢量图形设计、字体渲染等领域。贝塞尔曲线的核心是通过少量参数(控制点)灵活地创建复杂的平滑曲线,同时提供精确的数学描述。这个是目前最主流的,也算是最常用的,现在最新的231就基于这个来处理的,在生成能用的轨迹过后,在单独加上一些噪点即可,代码我就放在下面了
#!/usr/bin/env python
# -*- coding: UTF-8 -*-
import numpy as np
import math
import random
class bezierTrajectory:
def _bztsg(self, dataTrajectory):
lengthOfdata = len(dataTrajectory)
def staer(x):
t = ((x - dataTrajectory[0][0]) / (dataTrajectory[-1][0] - dataTrajectory[0][0]))
y = np.array([0, 0], dtype=np.float64)
for s in range(len(dataTrajectory)):
y += dataTrajectory[s] * ((math.factorial(lengthOfdata - 1) / (
math.factorial(s) * math.factorial(lengthOfdata - 1 - s))) * math.pow(t, s) * math.pow(
(1 - t), lengthOfdata - 1 - s))
return y[1]
return staer
def _type(self, type, x, numberList):
numberListre = []
pin = (x[1] - x[0]) / numberList
if type == 0:
for i in range(numberList):
numberListre.append(i * pin)
if pin >= 0:
numberListre = numberListre[::-1]
elif type == 1:
for i in range(numberList):
numberListre.append(1 * ((i * pin) ** 2))
numberListre = numberListre[::-1]
elif type == 2:
for i in range(numberList):
numberListre.append(1 * ((i * pin - x[1]) ** 2))
elif type == 3:
dataTrajectory = [np.array([0, 0]), np.array([(x[1] - x[0]) * 0.8, (x[1] - x[0]) * 0.6]),
np.array([x[1] - x[0], 0])]
fun = self._bztsg(dataTrajectory)
numberListre = [0]
for i in range(1, numberList):
numberListre.append(fun(i * pin) + numberListre[-1])
if pin >= 0:
numberListre = numberListre[::-1]
numberListre = np.abs(np.array(numberListre) - max(numberListre))
biaoNumberList = ((numberListre - numberListre[numberListre.argmin()]) / (
numberListre[numberListre.argmax()] - numberListre[numberListre.argmin()])) * (x[1] - x[0]) + x[0]
biaoNumberList[0] = x[0]
biaoNumberList[-1] = x[1]
return biaoNumberList
def getFun(self, s):
'''
:param s: 传入P点
:return: 返回公式
'''
dataTrajectory = []
for i in s:
dataTrajectory.append(np.array(i))
return self._bztsg(dataTrajectory)
def simulation(self, start, end, le=1, deviation=0, bias=0.5):
'''
:param start:开始点的坐标 如 start = [0, 0]
:param end:结束点的坐标 如 end = [100, 100]
:param le:几阶贝塞尔曲线,越大越复杂 如 le = 4
:param deviation:轨迹上下波动的范围 如 deviation = 10
:param bias:波动范围的分布位置 如 bias = 0.5
:return:返回一个字典equation对应该曲线的方程,P对应贝塞尔曲线的影响点
'''
start = np.array(start)
end = np.array(end)
cbb = []
if le != 1:
e = (1 - bias) / (le - 1)
cbb = [[bias + e * i, bias + e * (i + 1)] for i in range(le - 1)]
dataTrajectoryList = [start]
t = random.choice([-1, 1])
w = 0
for i in cbb:
px1 = start[0] + (end[0] - start[0]) * (random.random() * (i[1] - i[0]) + (i[0]))
p = np.array([px1, self._bztsg([start, end])(px1) + t * deviation])
dataTrajectoryList.append(p)
w += 1
if w >= 2:
w = 0
t = -1 * t
dataTrajectoryList.append(end)
return {"equation": self._bztsg(dataTrajectoryList), "P": np.array(dataTrajectoryList)}
def trackArray(self, start, end, numberList, le=1, deviation=0, bias=0.5, type=0, cbb=0, yhh=10):
'''
:param start:开始点的坐标 如 start = [0, 0]
:param end:结束点的坐标 如 end = [100, 100]
:param numberList:返回的数组的轨迹点的数量 numberList = 150
:param le:几阶贝塞尔曲线,越大越复杂 如 le = 4
:param deviation:轨迹上下波动的范围 如 deviation = 10
:param bias:波动范围的分布位置 如 bias = 0.5
:param type:0表示均速滑动,1表示先慢后快,2表示先快后慢,3表示先慢中间快后慢 如 type = 1
:param cbb:在终点来回摆动的次数
:param yhh:在终点来回摆动的范围
:return:返回一个字典trackArray对应轨迹数组,P对应贝塞尔曲线的影响点
'''
s = []
fun = self.simulation(start, end, le, deviation, bias)
w = fun['P']
fun = fun["equation"]
if cbb != 0:
numberListOfcbb = round(numberList * 0.2 / (cbb + 1))
numberList -= (numberListOfcbb * (cbb + 1))
xTrackArray = self._type(type, [start[0], end[0]], numberList)
for i in xTrackArray:
s.append([i, fun(i)])
dq = yhh / cbb
kg = 0
ends = np.copy(end)
for i in range(cbb):
if kg == 0:
d = np.array([end[0] + (yhh - dq * i),
((end[1] - start[1]) / (end[0] - start[0])) * (end[0] + (yhh - dq * i)) + (
end[1] - ((end[1] - start[1]) / (end[0] - start[0])) * end[0])])
kg = 1
else:
d = np.array([end[0] - (yhh - dq * i),
((end[1] - start[1]) / (end[0] - start[0])) * (end[0] - (yhh - dq * i)) + (
end[1] - ((end[1] - start[1]) / (end[0] - start[0])) * end[0])])
kg = 0
print(d)
y = self.trackArray(ends, d, numberListOfcbb, le=2, deviation=0, bias=0.5, type=0, cbb=0, yhh=10)
s += list(y['trackArray'])
ends = d
y = self.trackArray(ends, end, numberListOfcbb, le=2, deviation=0, bias=0.5, type=0, cbb=0, yhh=10)
s += list(y['trackArray'])
else:
xTrackArray = self._type(type, [start[0], end[0]], numberList)
for i in xTrackArray:
s.append([i, fun(i)])
return {"trackArray": np.array(s), "P": w}
a = bezierTrajectory()
r = a.trackArray(start=[830, 559], end=[1085, 554], numberList=30, le=4, deviation=0, bias=0.5, type=2, cbb=0,
yhh=0)
g = []
for i, l in enumerate(r['trackArray']):
s = {}
s['pageX'] = int(l[0])
s['clientX'] = int(l[0])
s['pageY'] = int(l[1])
s['clientY'] = int(l[1])
s['type'] = "mousedown" if i == 3 else "mousemove"
s['which'] = 1 if i == 3 else 0
g.append(s)
print(g)
结言
web风控千千万,轨迹占大头,这几种只是目前所在用的,还有一部分我就不放出来了,例如:高斯函数等一些更符合人体曲线的,这个函数同时加上几千条真实的ua指纹信息,同时都放到星球里面了,也欢迎大家来讨论。